QA系统问题中的常用指标
QA系统作为信息检索系统中的其中一种,其大致也通过信息检索系统的常用的指标进行性能评估。
其评价指标主要可以分为两类:
- 对单个查询进行评估的指标:对单个查询得到一个结果
- 对多个查询进行评估的指标(通常用于对系统的评价):求平均
单个查询的评价指标
P&R
召回率(Recall)=检出的相关文档数/相关文档数,也称为查全率,
准确率(Precision)=检出的相关文档数/检出文档数,也称为查准率,
例:某池塘有1400条鲤鱼,300只虾,300只鳖。现在以捕鲤鱼为目的。撒一大网,逮着了700条鲤鱼,200只虾,100只鳖。
正确率precision = 700 / (700 + 200 + 100) = 70%
召回率recall = 700 / 1400 = 50%
F值 = 正确率 召回率 2 / (正确率 + 召回率) (F 值即为正确率和召回率的调和平均值)
如果把池子里的所有的鲤鱼、虾和鳖都一网打尽,这些指标又有何变化:
正确率 = 1400 / (1400 + 300 + 300) = 70%
召回率 = 1400 / 1400 = 100%
F值 = 70% 100% 2 / (70% + 100%) = 82.35%
由此可见:
正确率是评估捕获的成果中目标成果所占得比例;
召回率,顾名思义,就是从关注领域中,召回目标类别的比例;
而F值,则是综合这二者指标的评估指标,用于综合反映整体的指标
在QA系统中,假设对3个正确答案7个错误答案组成的QA测试集进行分类,
召回率(Recall)=被系统分类为正确的答案个数/正确答案总数,
准确率(Precision)=被系统分类为正确的答案个数/分类问题总数,
F-Measure
当然希望检索结果Precision越高越好,同时Recall也越高越好,但事实上这两者在某些情况下有矛盾的:
比如极端情况下,我们只搜索出了一个结果,且是准确的,那么Precision就是100%,但是Recall就很低;而如果我们把所有结果都返回,那么比如Recall是100%,但是Precision就会很低。
P和R指标有时候会出现的矛盾的情况,这样就需要综合考虑他们,最常见的方法就是F-Measure(又称为F-Score)。
F-Measure是Precision和Recall加权调和平均:

当参数α=1时,就是最常见的F1,也即

可知F1综合了P和R的结果,当F1较高时则能说明试验方法比较有效。
Precision-Recall 曲线
因此在不同的场合中需要自己判断希望Precision比较高或是Recall比较高。
如果是做实验研究,可以绘制Precision-Recall曲线来帮助分析。

P-R曲线的优点:简单直观;既考虑了检索结果的覆盖度,又考虑了检索结果的排序情况
P-R曲线的缺点:单个查询的P-R曲线虽然直观,但是难以明确表示两个查询的检索结果的优劣。
AP Average Precision
对给定的任务和类别,precision/recall曲线以一种方法的排序输出来计算。Recall被定义为给定序列上所有正样本的部分;precision被定义为正类别序列上的所有样本。AP概括了precision/recall曲线的形状,被定义为在一组11个等间距recall水平[0, 0.1, 0.2,…,1]上的precision平均值。这意味着我们选择11个不同的置信度阈值(这决定序列)。置信度阈值的设定需要使recall值,即插值为0,0.1,0.2,…,1。
平均准确率AP是对不同召回率点上的正确率进行平均操作所得的结果:
- 未插值的AP: 某个查询Q共有6个相关结果,某系统排序返回了5篇相关文档,其位置分别是第1,第2,第5,第10,第20位,则AP=(1/1+2/2+3/5+4/10+5/20+0)/6 ;
- 插值的AP:在召回率分别为0,0.1,0.2,…,1.0的十一个点上的正确率求平均,等价于11点平均 ;
- 只对返回的相关文档进行计算的AP, AP=(1/1+2/2+3/5+4/10+5/20)/5,倾向那些快速返回结果的系统,没有考虑召回率。
NDCG Normalized Discounted Cumulative Gain
每个文档不仅仅只有相关和不相关两种情况,而是有相关度级别,比如0,1,2,3。
故可以假设,对于返回结果:
1、高关联度的结果比一般关联度的结果更影响最终的指标得分;
2、有高关联度的结果出现在更靠前的位置的时候,指标会越高;
NDCG(Normalized Discounted Cumulative Gain):计算相对复杂。对于排在结位置n处的NDCG的计算公式如下:
Gain:
正确度分成从0到r的r+1的等级(r可设定)。当取r=5时,等级设定如下图所示:

Cumulative Gain:
只考虑到了相关性的关联程度,没有考虑到位置的因素。它是一个搜素结果相关性分数的总和
举例:假设搜索“篮球”结果,最理想的结果是:B1、B2、 B3。而出现的结果是 B3、B1、B2的话,CG的值是没有变化的,因此需要下面的DCG。
例如现在有一个查询query={abc},返回下图左列的Ranked List(URL),当假设用户的选择与排序结果无关(即每一级都等概率被选中),则生成的累计增益值(从1到n的所有的位置上的贡献值都被加起来作为最终的评价结果,这样,一个一定长度的文档序列被转换成了一个相关分值的序列)。如下图最右列所示:

Discounted Cumulative Gain:
目的就是为了让排名越靠前的结果越能影响最后的结果。假设排序越往后,价值越低
考虑到一般情况下用户会优先点选排在前面的搜索结果,所以应该引入一个折算因子(discounting factor): 。那么第i个结果产生的效益就是:
引入相关影响度比重计算DCG:
这时将获得DCG值(Discounted Cumulative Gain)如下如所示:
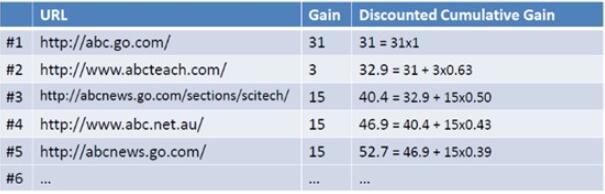
NDCG:
NDCG, Normalized 的DCG,由于搜索结果随着检索词的不同,返回的数量是不一致的,而DCG是一个累加的值,没法针对两个不同的搜索结果进行比较,因此需要归一化处理。
最后,为了使不同等级上的搜索结果的得分值容易比较,需要将DCG值归一化的到NDCG值。
操作如下图所示,首先计算理想排序后返回结果List的最大的MaxDCG值:
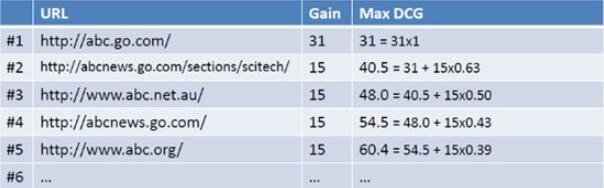
然后用DCG/MaxDCG就得到NDCG值,如下图所示:
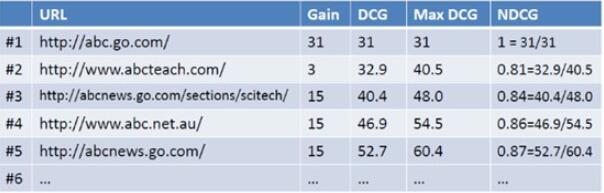
故如上图所示,NDCG@5 = 87%。
NDCG优点:图形直观,易解释;支持非二值的相关度定义,比P-R曲线更精确;能够反映用户的行为特征(如:用户的持续性persistence)
NDCG缺点:相关度的定义难以一致;需要参数设定
多个查询的评价指标
多个查询的评价指标,一般就是对单个查询的评价进行求平均。平均的求法一般有两种:
- 宏平均(Macro Average):对每个查询求出某个指标,然后对这些指标进行算术平均
- 微平均(Micro Average):将所有查询视为一个查询,将各种情况的文档总数求和,然后进行指标的计算
例如:
Micro Precision=(对所有查询检出的相关文档总数)/(对所有查询检出的文档总数)
宏平均对所有查询一视同仁
微平均受返回相关文档数目比较大的查询影响。
宏平均和微平均的例子:
两个查询q1、q2的标准答案数目分别为100个和50个,某系统对q1检索出80个结果,其中正确数目为40,系统对q2检索出30个结果,其中正确数目为24,则:
P1=40/80=0.5, R1=40/100=0.4
P2=24/30=0.8, R2=24/50=0.48
MacroP=(P1+P2)/2=0.65
MacroR=(R1+R2)/2=0.44
MicroP=(40+24)/(80+30)=0.58
MicroR=(40+24)/(100+50)=0.43
MAP
MAP(MeanAP :Mean Average Precision):对所有查询的AP求宏平均。具体而言,单个主题的平均准确率是每篇相关文档检索出后的准确率的平均值。主集合的平均准确率(MAP)是每个主题的平均准确率(AP)的平均值。
MAP 是反映系统在全部相关文档上性能的单值指标。系统检索出来的相关文档越靠前(rank 越高),MAP就可能越高。如果系统没有返回相关文档,则准确率默认为0。
多个查询下的查准率/查全率曲线,可通过计算其平均查准率得到,公式如下(Nq为查询的数量) :
P(r) 是指查全率为r时的平均查准率, Pi(r)指查全率为r时的第i个查询的查准率 。
例如:假设有两个主题,主题1有4个相关网页,主题2有5个相关网页。某系统对于主题1检索出4个相关网页,其rank分别为1, 2, 4, 7;对于主题2检索出3个相关网页,其rank分别为1,3,5。对于主题1,平均准确率为(1/1+2/2+3/4+4/7)/4=0.83。对于主题2,平均准确率为(1/1+2/3+3/5+0+0)/5=0.45。则MAP= (0.83+0.45)/2=0.64。
MRR
MRR(Mean Reciprocal Rank) :对于某些IR系统(如问答系统或主页发现系统),只关心第一个标准答案返回的位置(Rank),越前越好,这个位置的倒数称为RR,对问题集合求平均,则得到MRR。(把标准答案在被评价系统给出结果中的排序取倒数作为它的准确度,再对所有的问题取平均)
例一:两个query,系统对第一个问题返回的标准答案的Rank是2,对第二个问题返回的标准答案的Rank是4,则系统的MRR为(1/2+1/4)/2=3/8
再举个例子:有3个query如下图所示:(黑体为返回结果中最匹配的一项)
可计算这个系统的MRR值为:(1/3 + 1/2 + 1)/3 = 11/18=0.61。
该指标计算的是:
在给定n个候选答案的情况下,抽取最匹配(best-matched)的k个答案,计算这k个答案中正确答案的召回率



